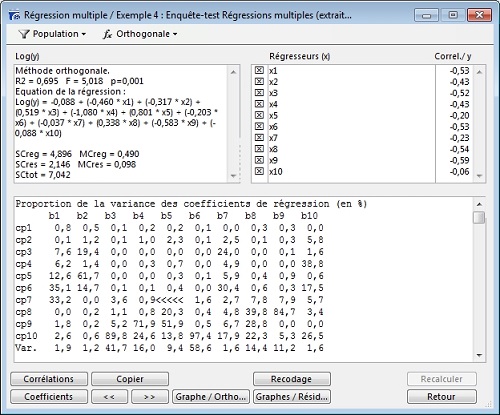
Ce tableau nous permet de connaître, pour chaque composante, sa contribution (en pourcentage) à la variance d’un coefficient. Les composantes principales sont classées dans l’ordre croissant de leur variabilité (la 10é composante est la composante à la plus faible variabilité).
Ce tableau présente un double intérêt en ce sens qu’il :
indique les composantes responsables d’une inflation importante de la variance d’un coefficient (voir inflation de R2)
et qu’il permet de détecter la présence de colinéarité entre les variables explicatives
Ainsi, ci-dessus nous constatons que la 10è composante est responsable de 89,8% de la variance du coefficient b3, de 97,4% de la variance du coefficient b6, et que la 9é composante est, elle, responsable de 71,9% de la variance du coefficient b4 et de 51,9% de celle du coefficient b5.
Ce tableau propose un autre avantage, à savoir celui de déterminer l’existence de colinéarité entre certaines variables. Avant d’interpréter hâtivement les résultats du tableau ci-dessus, il est important de connaître la contrainte suivante, à savoir que pour pouvoir conclure à la colinéarité ou quasi colinéarité de plusieurs variables, il est indispensable qu’au moins deux variances soient affectées dans de fortes proportions par une même composante.
Ainsi, nous pouvons conclure d’après les résultats ci-dessus à une quasi-colinéarité, voire colinéarité des variables X3 et X6, de même pour les variables X4 et X5 bien qu’elles le soient d’un degré moindre.
