Un modèle général de régression linéaire multiple comprenant p variables s’écrit comme suit: Yi = b0+b1X1+b2X2+…+bPXP+ui où i = 1,2,…,n
Avec :
Yi : variable expliquée (à expliquer)
Xi : variable explicative
bi : paramètres à estimer
ui : erreur aléatoire non observable
La méthode de régression multiple va estimer les paramètres bi . La première chose à effectuer étant de tester la validité du modèle à travers l’analyse des résidus.
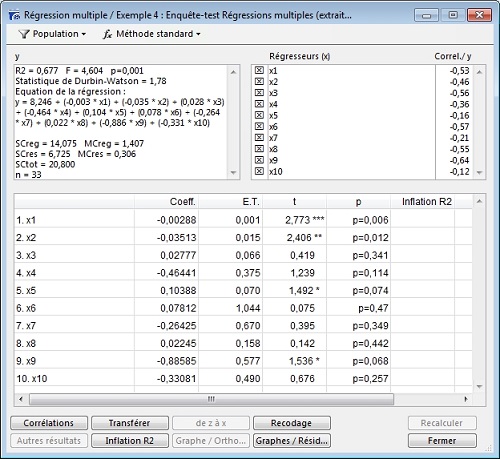
L’équation de régression linéaire multiple est de la forme : Y = b0+b1 X1 + b2 X2 +…+ bi Xi
Cette équation nous donne les estimations des paramètres bi, c’est-à-dire les coefficients des régresseurs, calculés à travers la Méthode des Moindres Carrés Ordinaires, qui consiste à minimiser la somme des carrés des résidus.
De manière générale, chaque bi est interprété comme l’accroissement de Y correspondant à l’accroissement d’une unité de Xi lorsque toutes les autres variables sont maintenues constantes. Le signe de chaque coefficient permet de connaître le sens de variation entre Y et Xi.
