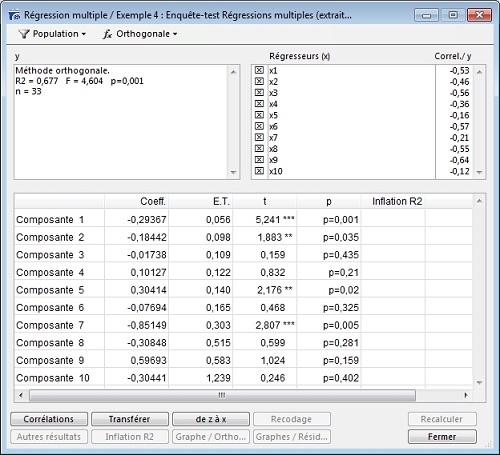
La méthode de régression orthogonalisée présente les deux avantages suivants :
1) elle permet de pouvoir » écarter » un problème de structure des variables explicatives, à savoir la non orthogonalité de celles-ci
2) elle permet à l’utilisateur de sélectionner un sous-ensemble de variables explicatives en fonction de la stabilité de leur coefficient afin de créer un modèle de bonne qualité
Le principe de la méthode de régression orthogonalisée est, dans un premier temps, de transformer les variables explicatives en composantes principales, c’est-à-dire en variables orthogonales deux à deux, et ensuite d’effectuer une régression sur ces nouvelles variables.
Modalisa ne permettant pas de pouvoir interpréter ces composantes, il est alors nécessaire de revenir aux variables initiales (cliquer » Z vers X « ), tout en sachant qu’une modification d’échelle aura été effectuée : les nouveaux coefficients de régression seront les coefficients des variables initiales réduites.
L’intérêt d’utiliser la méthode de régression orthogonalisée est donc de pouvoir sélectionner un certain nombre de variables qui constitueront un nouveau modèle de bonne qualité, grâce à la stabilité de ses coefficients.
Il est nécessaire, dans le cadre de la régression orthogonalisée, d’analyser le tableau présentant l’évolution des valeurs des » Coefficients en fonction du nombre de composantes » et le graphique correspondant (Graphe/Orthogo) afin de pouvoir sélectionner les variables stables du modèle.
