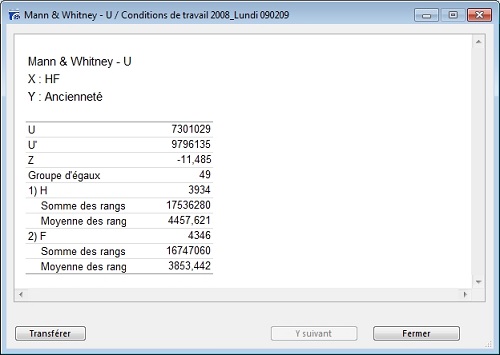
Le test Mann et Whitney U permet d’effectuer la comparaison de deux échantillons indépendants, de faibles effectifs, ne vérifiant pas la condition de « normalité » (la forme de la distribution ne présente pas une courbe « en cloche », courbe de Gauss). Ce test s’applique essentiellement sur des variables ordinales.
Démarche : les valeurs des deux échantillons sont rassemblées en un même groupe, puis converties par numéros d’ordre en rang. Les deux échantillons sont alors reconstitués et on calcule pour chacun la somme des rangs.
L’hypothèse nulle est alors la suivante : la somme des rangs pour l’échantillon 1 est analogue à la somme pour l’échantillon 2.
L’hypothèse nulle (Ho) est acceptée si U’, la valeur du test observée, est inférieur à U, valeur du test au seuil de significativité de 5%. Inversement, l’hypothèse nulle est rejetée si U’>U.
Ci-dessus, U'(9796135)>U(7301029), Ho est rejetée, on observe que les hommes ont plus d’ancienneté que les femmes, au sein de la population des personnels de l’entreprise.
