Un intervalle de confiance permet d’évaluer le degré de précision des analyses statistiques réalisées sur un échantillon de population.
Pour des raisons pratiques et économiques, quand on réalise une enquête, la plupart du temps on interroge plutôt un échantillon que la population totale concernée. Cette non-exhaustivité entraine un manque de précision : en effet, il existe un écart entre la valeur d’une variable observée pour l’ensemble d’une population de référence et la valeur observée pour un échantillon de cette population.
L’intervalle de confiance est la prise en compte de la marge d’erreur entre la valeur observée pour l’échantillon et sa généralisation possible à la population de référence. C’est l’intervalle dans lequel la valeur de la variable a une forte probabilité de se trouver.
On le note ainsi : Estimation – marge < Vraie Valeur < Estimation + marge
Cet encadrement ne peut être utilisé qu’à la condition que la distribution de la population totale est normale (elle décrit une courbe de Gauss).
Plus l’écart-type de la distribution de la variable est important plus l’intervalle de confiance est large.
Plus l’échantillon est grand, plus l’intervalle de confiance diminue.
Plus le risque d’erreur consenti est grand, plus l’intervalle de confiance est petit.
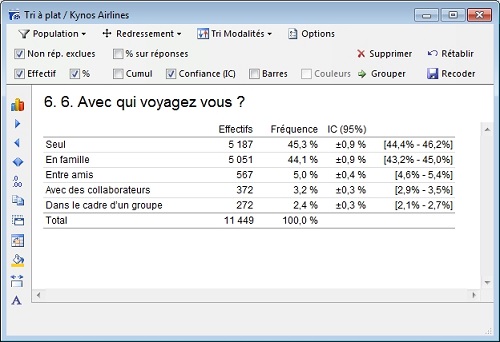
Dans notre exemple, le niveau de confiance est 95%, le seuil de risque s’élève à 5% : il y a 2,5% de chance que la vraie valeur se situe en dessous de l’intervalle et 2,5% au dessus, et il est probable que 95 fois sur cent le nombre de personnes voyageant en groupe se situera entre 2,1 et 2,7% de la population générale.
