Le test de Friedman est un test non-paramétrique qui permet d’effectuer la comparaison de plus de deux échantillons appareillés.
Ce test s’applique le plus souvent sur des échantillons de faible effectif, et/ou ne vérifiant pas la condition de normalité, c’est-à-dire que la forme de leur distribution ne présente pas une courbe « en cloche ». Les données observées sont essentiellement des variables ordinales et des données qualitatives, voire des données numériques transformées en classes ordonnées le cas échéant (si la distribution ne suit pas la loi normale notamment).
Interprétation :
– Les valeurs sont classées par numéro d’ordre et par groupe.
– Les valeurs sont ensuite redistribuées sur chaque échantillon, la somme des rangs étant calculée pour chacun.
– La valeur H (non-affichée sur Modalisa) est comparée à la valeur théorique lue dans la table des distributions Khi2 de Pearson.
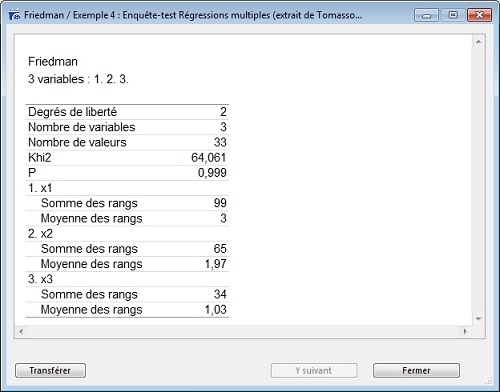
Dans l’exemple ci-dessus, l’hypothèse nulle (Ho) est la suivante : l’appréciation du contenu du stage n’évolue pas avec le temps. La probabilité doit être supérieure ou égale à p=0,05. Ici, p=0,999 donc la condition de l’hypothèse nulle est rejetée : l’appréciation du contenu est différente selon les différents moments du stage.
