Moyenne du produit des écarts de deux variables à leur moyenne respective, cet indice statistique est pris en compte dans le calcul du coefficient de corrélation.
La covariance permet d’estimer le sens de la variation entre deux variables numériques et ainsi d’estimer l’indépendance de ces variables :
– Si la covariance est de signe positif, les variables varient dans le même sens (ou covarient) : les sujets qui ont des valeurs fortes (au dessus de la moyenne) sur une variable, présentent également des valeurs élevées sur l’autre variable.
– Si la valeur de la covariance est de signe négatif cela signifie que les variables varient en sens inverse : les sujets qui ont des valeurs fortes sur une des deux variables auront tendance à avoir des valeurs faibles sur l’autre variable.
– Si la valeur de la covariance est proche de la valeur 0, cela signifie que les variables ne covarient pas : parmi les sujets présentant des valeurs fortes sur une variable, on peut observer que, sur l’autre variable, ces mêmes sujets présentent des valeurs fortes, faibles ou moyennes.
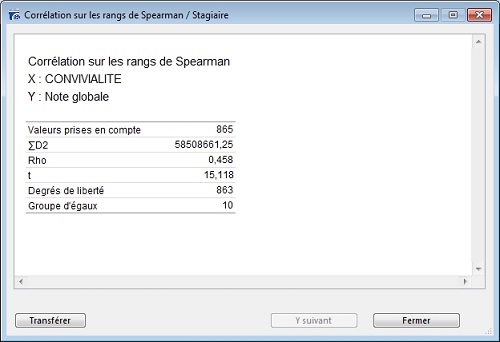
Dans l’exemple ci-dessus, la variance est de signe positif (Rho = + 0,458). Cela signifie que si un individu a donné une note de convivialité élevée, il aura donné une note gloable élevée également.
