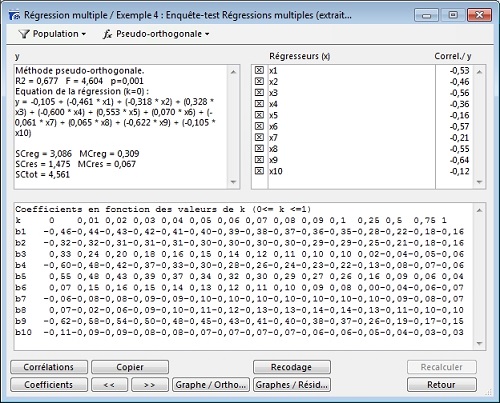
Ce tableau présente les valeurs des coefficients de la régression pseudo-orthogonalisée en fonction des différentes valeurs de k. Il nous permet de constater l’évolution de ces valeurs pour pouvoir ainsi conclure ou non à la stabilité des coefficients.
En faisant varier k, Modalisa limite progressivement les effets dus à la quasi-colinéarité des variables explicatives. Cet avantage est malheureusement contrebalancé par un aspect quelque peu négatif : le biais des estimations. En effet, plus k augmente, plus le biais augmente et plus les coefficients tendent vers 0.
Modalisa utilise les valeurs de ce tableau afin de construire un graphique dont l’analyse permet de constater plus simplement l’évolution des valeurs des coefficients.
Une fois les coefficients instables déterminés, il s’agit d’éliminer d’une part les variables explicatives dont les coefficients sont instables et tendent vers 0, et d’autre part celles dont les coefficients sont faibles.
Si nous étudions les valeurs proposées par le tableau ci-dessus, il s’agira d’éliminer les variables explicatives suivantes : X3, X6, X7, X8 et X10. En demandant à Modalisa d’effectuer une nouvelle régression en ne conservant dans le modèle que les variables explicatives X1, X2, X4, X5 et X9, vous pourrez constater que le coefficient de X9 n’est pas significativement différent de 0, il s’agira alors d’éliminer X9 du modèle pour obtenir le modèle final et s’apercevoir que la régression pseudo-orthogonalisée a eu pour effet de limiter les effets de X4 et X5 (variables colinéaires) sans pourtant les éliminer comme le fait la régression orthogonalisée.
