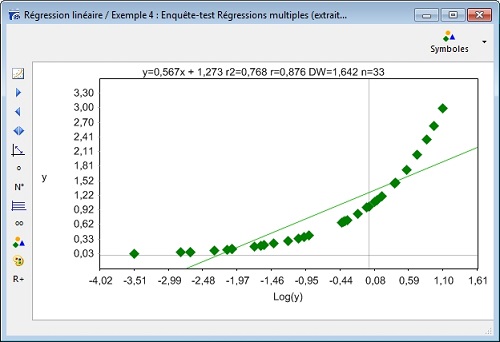
L’analyse de régression linéaire simple est un outil qui permet d’étudier la relation existant entre deux variables : quand cette relation peut être représentée par une droite de régression, on parle de régression linéaire, ce qui signifie que la variable dépendante dépend linéairement d’une seule variable indépendante.
La variable dépendante est la variable que l’on veut expliquer : elle est également appelée variable régressée. La variable qui explique les variations de la variable dépendante est appelée variable indépendante ou régressante ou explicative.
On affecte généralement l’axe des « x » à la variable explicative et des « y » à la variable à expliquer.
Équation, ou représentation graphique (la Droite des Moindres Carrés), permettant l’étude de la liaison entre deux variables numériques :
– L’équation de la droite est de type y= ax+b avec a= pente, b= la valeur de y quand x= 0.
– La pente de la droite (a) indique le sens de la liaison entre les deux variables.
– Le coefficient de détermination r2 permet d’évaluer la force de la liaison.
En cas de liaisons positives ou négatives entre les deux variables, la droite de régression devient un indice pronostique qui permet d’estimer les valeurs de Y en fonction des valeurs de X (la taille en fonction du poids). En résumant sur un graphique la liaison entre les deux variables, on peut par exemple prédire qu’un individu pesant 65 kg mesurera environ 1,70 mètre. Plus la liaison (coefficient de corrélation) sera forte, plus la prédiction sera précise et fiable.
